Setiap uji validitas tentu memiliki dasar dalam pengambilan keputusan sebagai acuan untuk membuat kesimpulan adapun dasar pengambilan keputusan dalam uji validitas bisa dilakukan melalui beberapa cara yaitu:

Membandingkan nilai r-hitung dengan nilai r-tabel

1. Apabila nilai r-hitung > r-tabel, maka item soal angket dinyatakan valid

2. Apabila nilai r-hitung < r-tabel, maka item soal angket dinyatakan tidak valid.

 

Adapun tabulasi data jawaban responden dapat dilihat dibawah ini:

NB: Tabulasi perlu diberi Total skor seperti gambar di atas

Data tabulasi tersebut di copy dan di paste di program SPSS seperti gambar di bawah ini:

 

Klik Variable view (dibagian pojok kiri bawah) dan kemudian ubah data default seperti contoh dibawah:

Pilih Data View

1. Dari baris menu pilih Analyze, kemudian pilih Correlate, lalu pilih Bivariate.
2. Blog smua VAR terus pindah ke kanan seperti tampilan di bawah 

3. Selanjutnya akan muncul output hasilnya. Tinggal di lihat hasil tersebut untuk menentukan item pertanyaan yang valid dan tidak valid dengan r-tabel

Pada tabel di atas dapat dilihat pada pearson correlation (r-hitung) di skor totalnya dibandingkan dengan r-tabel.

Contoh : tabulasi memiliki 30 Peserta didik untuk di uji cobakan yang r-tabelnya yaitu 0,361

Apabila melihat item pernyataan nomor 1 yang memiliki r-hitung 0,886 > 0,361 (r-tabel) artinya soal valid.

Dan dilihat pada nomer item selanjutnya.

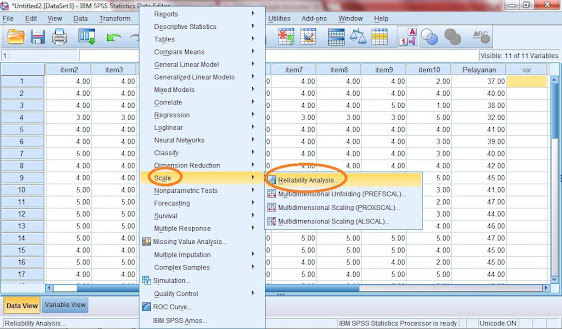
Pengujian Reliabilitas

1. Klik menu analyze

2. pilih scale

3. pilih reliability analysis

Sehingga muncul tampilan

Pindahkan ke kanan seperti gambar dibawah ini:

Klik OK dan muncul tampilan hasil reliabilitas

Reliabilitas memiliki hasil sebanyak 0,818 yang artinya angket sudah reliabilitas atau dapat dipercaya.

Keputusan uji reliabilitas apabila r₁₁ > r tabel, maka intrumen reliabel atau dapat dipercaya. Adapun kategorinya sebagai berikut: (Azwar, Saifuddin. 2014. Penyusunan Skala Psikologi. Yogyakarta: Pustaka Pelajar)

Kategori	interval
Sangat Tinggi	0,81-1,00
Tinggi	0,61-0,80
Cukup Tinggi	0,41-0,60
Rendah	0,21-0,40
Sangat Rendah	0,00-0,20

 

 

Uji normalitas merupakan suatu distribusi yang menunjukkan sebaran data yang seimbang sebagian besar data berada pada nilai di tengah. Normalitas merupakan syarat keharusan dan pertama pada analisis parametrik dan analisis regresi. Uji normalitas bertujuan untuk menguji apakah dalam model regresi, variabel penggangu atau residual memiliki distribusi normal.  Jika asumsi ini dilanggar, maka uji statistik menjadi tidak valid atau bias terutama untuk sampel kecil. Uji normalitas dapat dilakukan melalui dua pendekatan yaitu  secara deskriptif dan inferensia.

pengujian hasil nilai normalitas terdapat ketentuan kriteria yaitu Apabila nilai sig ≤ 0,05 maka data berdistribusi tidak normal. Apabila nilai sig ≥ 0,05 maka data berdistribusi normal.

 

Uji normalitas bertujuan untuk mengukur suatu penelitian ke uji statistik parametrik atau non-parametrik

Apabila data berdistribusi normal maka uji statistik yang digunakan adalah uji statistik parametrik dengan teknik uji t, namun apabila data menunjukkan distribusi tidak normal maka yang digunakan adalah statistik non-parametrik dengan teknik uji wilcoxon. Berikut tutorial uji normalitas menggunakan SPSS:

 

Buka data tabulasi pretest dan postest dari excel dan blog kedua tabel tersebut, serta copy dan buka jendele excel baru Klik kanan di atas sel kiri atas tempat Anda ingin menempelkan tabel yang telah di transpose, lalu pilih Ubah 

maka akan tampil tabel seperti di atas.

Data tabulasi tersebut di copy dan di paste di program SPSS seperti tampilan di bawah ini:

Dari baris menu pilih Variable View, kemudian ubah data default seperti contoh dibawah:

1. Pilih Data View

1. Dari baris menu pilih Analyze, kemudian pilih Decriptive statistic, Explore. 
2.  Masukan Variabel tradisional  ke dalam dependent list.
3.  Pilh kotak plots, kemudian pilih Factor levels together pada boxplot(untuk menampilkan boxplot), pilih Histogram pada Descriptive (untuk menampilkan histogram) dan Normality Plots with test (untuk menampilkan plot dan uji normalitas). Akan terlihat tampilan sebagai berikut:

 

 

 Diatas menunjukkan hasil data uji normalitas yaitu di uji kolmogrov data signifikansi yaitu 0,000 ≤ 0,05 yang artinya data tidak berdistribusi normal

Jadi data tersebut menggunakan uji statistik non-parametrik dengan teknik uji wilcoxon

Contoh data berdistribusi normal dapat dilihat dibawah ini:

Data di atas pada uji kolmogrov menunjukkan data nilai sig 0,200 ≥ 0,05 artinya data berdistribusi normal dan disebut dengan uji statistik parametrik yang dapat menggunakan teknik uji t

Prososial Arnold P. Goldstein, Edward G. Carr and William S. Davidson by faiz on Scribd

PROSOSIAL Paul W.B. Atkins PhD, David Sloan Wilson PhD, Steven C. Hayes PhD by faiz on Scribd

Kerjasama Group Play Interventions by faiz on Scribd

Kerja Sama - Joining Together_ Group Theory and Group Skills Johnson, David W_Johnson, Frank P (2013) by faiz on Scribd

Albert Bandura Self-Efficacy by faiz on Scribd

motivasi belajar by faiz on Scribd